Por que você deve sempre visualizar seus dados
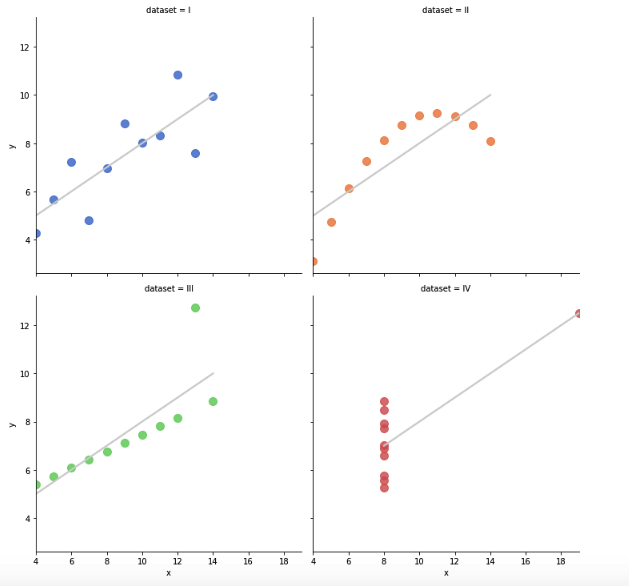
Quarteto de Anscombe: Visualizando os gráficos de dispersão abaixo, você imaginaria que os quatro resultam em estatísticas descritivas praticamente idênticas?
Nem eu! 🤪
Por isso, resolvi buscar os dados, plotá-los e visualizar algumas estatísticas.
Para saber mais, continue lendo este artigo e se tiver algum comentário ou sugestão, deixe lá no final, na caixa de mensagens 😁
Vamos lá!
Se você quiser, pode acompanhar o notebook no repositório no Github abaixo:
Quarteto de Anscombe
Acesse o notebook aqui!
O quarteto de Anscombe foi construído por um estatístico inglês chamado… Francis Anscombe 😛
Basicamente, o conjunto de dados possui algumas características que podem “enganar” uma regressão linear.
O estudo também é muito discutido quando falamos sobre a importância da visualização de dados. Somente quando são plotados que notamos uma grande diferença. Na verdade, notamos que os dados possuem comportamentos totalmente diferentes.
Obs: O objetivo deste artigo não é falar sobre Regressão Linear e/ou como interpretar os modelos. Se você quiser saber mais, recomendo muito esta playlist no Youtube (em inglês): Simple Linear Regression.
O livro da série “Use a cabeça” – Análise de Dados aborda regressão linear de forma bastante didática (na verdade, o livro todo tem vários exemplos e conceitos introdutórios bem simples de entender). Você pode adquirir o livro no site da Amazon clicando aqui.
Voltando ao Quarteto de Anscombe, a biblioteca Seaborn possui o método que nos permite visualizar e estudar estes dados.
Vamos importar o dataset e atribuí-lo na variável “df”:
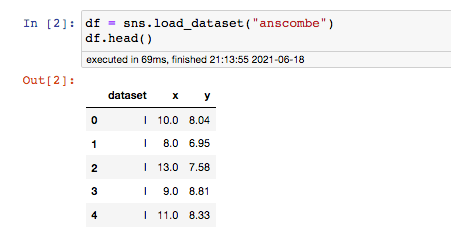
Com 44 linhas e 3 colunas, o dataset é bem simples e os números não diferem muito entre si.
Temos 4 “datasets” diferentes, que vai do I até o IV. O menor valor do nosso eixo X é 4 e o máximo 19. Para os valores Y, o range não chega a 10 (mínimo 3.1 e máximo de 12.74).

Para visualizarmos algumas estatísticas, criei uma função que resulta em uma regressão simples para cada um dos valores na variável (coluna) dataset.

Quer melhorar seu histograma utilizando a biblioteca Seaborn? Clique aqui e leia o artigo completo:
Agora, vamos usar a função em nosso Anscombe’s dataset, armazenar cada um dos resultados e compará-los:
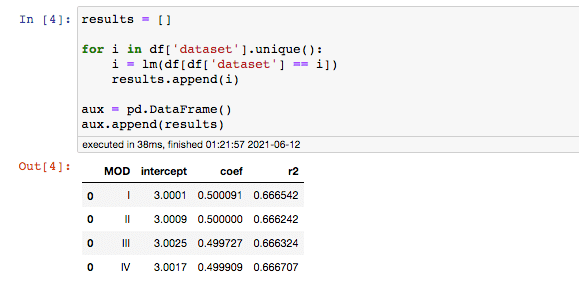
Como podemos ver no DataFrame acima (DataFrame “aux”), os valores de B0 e B1 diferenciam muito pouco em cada um dos testes. Se formos considerar o arredondamento então, é praticamente nada.
Analisando somente a estatística básica, como média, variância e os resultados da regressão linear, como o intercepto e coeficiente de determinação, não vemos praticamente nenhuma diferença.
Mas quando plotamos os dados…

Analisando os plot’s, vemos que o modelo 01 se ajusta muito bem a um modelo de regressão linear.
O comportamento dos dados do modelo 02 se mostra não linear e a diferença fica ainda mais clara no último plot com dados que uma regressão linear não poderia explicar.
Claro que os dados se tratam de um estudo e na vida real, é praticamente impossível nos depararmos com uma situação exatamente igual a esta. Embora possa parecer simples, o quarteto de Anscombe’s é muito interessante para percebermos a importância da visualização de dados e como, matematicamente, nossos modelos podem se enganar.
Se estiver algum comentário, não se esqueça de deixar nos comentários aqui abaixo 👇 👇